Endianness and the coin toss
2017-10-30
I’m trying to better understand where endianness comes from and its impacts on code performance. Here’s what I’ve got so far.
Description
First, here’s how integer 0x0A0B0C0D, or 168496141, is stored in little-endian and big-endian.
In little-endian, the least significant bytes come first:
address | byte value
--------------------
0x00 | 0x0D -> least significant
0x01 | 0x0C
0x02 | 0x0B
0x03 | 0x0A
In big-endian, the most significant bytes come first:
address | byte value
--------------------
0x00 | 0x0A -> most significant
0x01 | 0x0B
0x02 | 0x0C
0x03 | 0x0D
Network performance
Endianness is somewhat linked to network, because network byte order is always big-endian. So I wonder if endianness could have an impact on networking code performance.
The question “What are the pros and cons of little-endian versus big-endian?” on Quora seems to indicate that neither one is better than the other. In addition, the Intel 64 instruction set has a BSWAP instruction that is specially made to convert integers from big-endian to little-endian and vice-versa. So even with an x64 CPU, endianness looks to be heavily optimized.
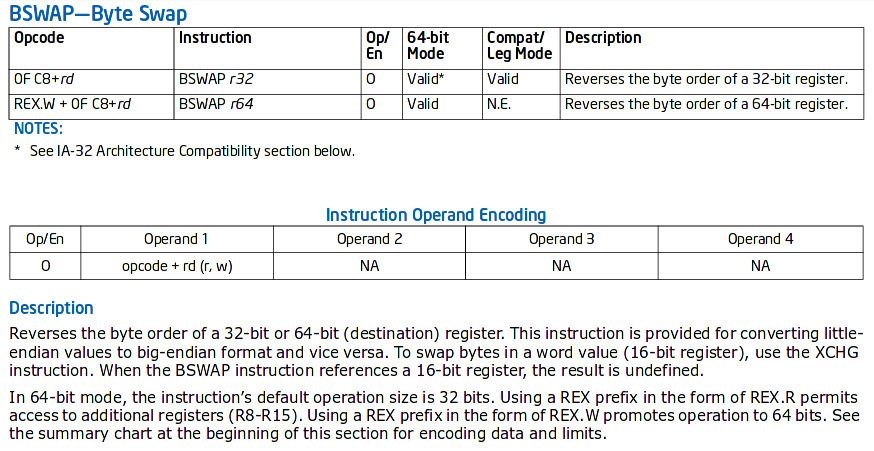
This instruction is used by the operating system kernels. For instance, on my Arch Linux installation, BSWAP appears in the /usr/include/bits/byteswap.h header:
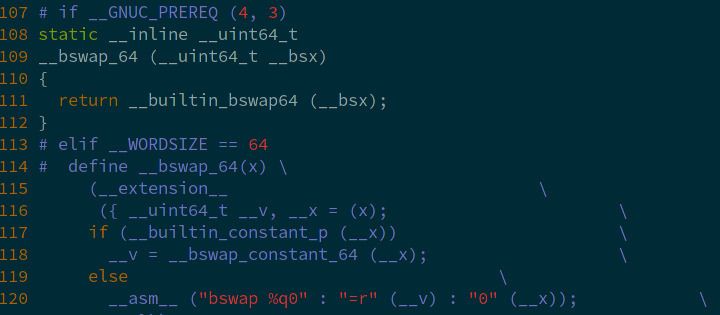
I trust that Intel optimizes these functions as much as possible. So I suppose the performance impact of calling BSWAP is small. In addition, there are several cases where swapping byte order can be completely avoided:
- big-endian machines already use network byte order internally, so they don’t need to swap byte order before sending data off to the network;
- little-endian machines that talk to each other over TCP do not need to swap bytes since the bytes are read in-order on the receiving end.
The only case where endianness should really cause slow down is if a big-endian machine talks with a little-endian machine.
Math and typecasts
Akash Sharma makes a good point for little-endian. He explains how little-endian makes common maths operations easier:
Consider an example where you want to find whether a number is even or odd. Now that requires testing the least significant bit. If it is 0 it is even. In Little Endian Ordering least significant byte is stored at starting address. So just retrieve the byte and look at its last bit. — Akash Sharma
And how little-endian makes typecasts to smaller types easier:
For example you want to typecast a 4 bytes data type to 2 bytes data type. In Little Endian Ordering it is pretty straightforward as you just need to retrieve the first 2 bytes from starting address in order and you would get the correct number. — Akash Sharma
Consistency and the coin toss
The paper “On holy wars and a plea for peace” by Danny Cohen also gives some interesting background behind the decision to use big-endian for network byte order. This paper is referenced in rfc1700 which defines network byte-order.
Cohen’s paper points to the inconsistency of some little-endian systems back in the eighties, when the paper was written:
Most computers were designed by Big-Endians, who under the threat of criminal prosecution pretended to be Little-Endians, rather than seeking exile in Blefuscu. They did it by using the B0-to-B31 convention of the Little-Endians, while keeping the Big-Endians’ conventions for bytes and words. — Danny Cohen
This sounds like a joke, but Cohen goes on to describe how the M68000 microprocessor was little-endian for bits but big-endian for words (bytes), double-words and quad-words. And it points to the better consistency of some big-endian systems:
The PDP10 and the 360, for example, were designed by Big-Endians: their bit order, byte-order, word-order and page-order are the same. The same order also applies to long (multi-word) character strings and to multiple precision numbers. — Danny Cohen
Finally, it ends by saying that making a decision and having all computer scientists agree on it will be extraordinarily difficult. For this reason, it suggests:
How about tossing a coin ??? — Danny Cohen
Almost 40 years later, the network folks settle for big-endian and the majority-share CPUs (x86, arm) are little-endian. In software development though, the choice is not clear. Luckily, there is probably no need to worry about bit-endianness, only byte-endianness. Partial win, I guess.